AceFEM

The AceFEM package is a general finite element environment designed to solve multi-physics and multi-field problems. The AceFEM package explores advantages of symbolic capabilities of Mathematica while maintaining numerical efficiency of commercial finite element environment. The package combines use of Mathematica’s facilities with external handling of intensive computations by compiled modules.

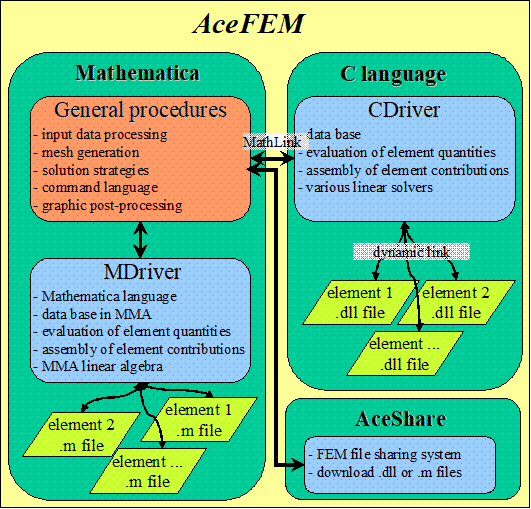
The main part of the package includes procedures that are not numerically intensive, such as processing of the user input data, mesh generation, control of the solution procedures, graphic post-processing of the results, etc.. Those procedures are written in Mathematica language and executed inside Mathematica. The numerical module includes numerically intensive operations, such as evaluation and assembly of the finite element quantities (tangent matrix, residual, sensitivity vectors, etc.), solution of the linear system of equations, contact search procedures, etc.. The numerical module exists as Mathematica package as well as external program written in C language and is connected with Mathematica via the MathLink protocol. This unique capability gives the user the opportunity to solve industrial large-scale problems with several 100000 unknowns and to use advanced capabilities of Mathematica such as high precision arithmetic, interval arithmetic, or even symbolic evaluation of FE quantities to analyze various properties of the numerical procedures on relatively small examples. The AceFEM package comes with a library of finite elements (solid, thermal, contact,... 2D, 3D,...) including full symbolic input for most of the elements. Additional elements can be accessed through the AceShare finite element file sharing system. The element oriented approach enables easy creation of costumized finite element based applications in Mathematica. In combination with the automatic code generation package AceGen the AceFEM package represents an ideal tool for a rapid development of new numerical models.

Unique features found in the product

Duality

• The AceFEM package explores the advantages of symbolic capabilities of Mathematica while maintaining numerical efficiency of commercial finite element environment. The unique solution has been achieved, not shared by other products, thorough splitting the package into three parts. The main part is written in Mathematica and includes procedures that are not numerically intensive The numerical module that includes numerically intensive operations is dual symbolic/numeric and exists as Mathematica package as well as external program written in C language and is connected with Mathematica via the MathLink protocol.
• Semi analytical and large scale simulations share the same pre-processing, post-processing and solution control procedures.
• During the FEM analysis there is all the time full access to all environment data, nodal data and element data as well as solution procedure. They can be accessed and changed directly from Mathematica (MathLink). This gives AceFEM flexibility that is not shared by other FE environments.

Element oriented technology

• In the last decade or so the use of object oriented approach has been considered as the main method of obtaining reusable and extensible numerical software. Only the shift of complexity of data management is performed by utilizing object oriented approach, while the level of abstraction of the problem description remains the same. With the use of symbolic tools and automatic code generation a new, more flexible approached can be introduced. The symbolic approach can bypass the drawbacks of the OO formulation by abandoning the re-usable codes concept and providing only the basic functionality at the global level of the finite element environment which is manually coded.
• The codes at the local level of the finite element are automatically generated, self-contained and connected to the Mathematica through MathLink. The MathLink connection is provided in both directions. The user can, during the analysis session, directly change the data contained within the elements from Mathematica. Additionally, the element code can also contain bits of Mathematica input that can influence the mesh generation, solution procedure and post-processing.
• The AceFEM enables easy creation of customized finite element based applications in Mathematica.
• In combination with the automatic code generation package AceGen the AceFem package represents an ideal tool for a rapid development of new numerical models.
• The AceFEM environment comes with a small build-in library including standard solid, structural, thermal and contact elements. Additional elements are accessed and automatically downloadable through the AceShare system.
• The AceFEM supports analytical sensitivity analysis for all elements (including large strain plasticity!!).

NOTE: The complementary product AceGen is required for the generation of new finite elements. Without AceGen only the existing elements from the built-in or shared libraries can be used!

References

· ZUPAN, Nina, KORELC, Jože. Sensitivity analysis based multi-scale methods of coupled path-dependent problems, Computational Mechanics, 2020, 65:229–248, DOI 10.1007/s00466-019-01762-8, https://link.springer.com/article/10.1007/s00466-019-01762-8

· Research Challenges in Mechanics: Applications of Automated Computational Modeling , https://www.rcm2017.uni-hannover.de/

· ZUPAN, Nina, KORELC, Jože. Unified approach to sensitivity analysis based automation of multiscale modelling. V: SORIĆ, Jurica (ed.), WRIGGERS, Peter (ed.), ALLIX, Olivier (ed.). Multiscale modeling of heterogeneous structures, (Lecture notes in applied and computational mechanics, ISSN 1613-7736, Vol. 86). Berlin: Springer International Publishing AG. cop. 2018, 113-127

· KORELC, Jože, WRIGGERS, Peter. Automation of finite element methods. Switzerland: Springer, 2016. XXVI. http://link.springer.com/book/10.1007%2F978-3-319-39005-5, doi: 10.1007/978-3-319-39005-5. http://www.springer.com/-/1/AVXo2wyFKEAfyFF0Zyqj

· AceGen and AceFEM manual and installation, http://symech.fgg.uni-lj.si/

· STANIĆ, Andjelka, BRANK, Boštjan, KORELC, Jože. On path-following methods for structural failure problems. Computational mechanics, ISSN 0178-7675, 2016, letn. 57, št. v tisku, str. 1-26, ilustr., doi: 10.1007/s00466-016-1294-y. [COBISS.SI-ID 7456097]

· HUDOBIVNIK, Blaž, KORELC, Jože. Closed-form representation of matrix functions in the formulation of nonlinear material models. Finite Elements in Analysis and Design, 2016, 111:19-32

· ŠOLINC, Urša, KORELC, Jože. A simple way to improved formulation of FE2 analysis. Computational mechanics, 2015, 56:905-915, doi: 10.1007/s00466-015-1208-4. [COBISS.SI-ID 7244129]

· MELINK, Teja, KORELC, Jože. Stability of Karhunen- Loève expansion for the simulation of Gaussian stochastic fields using Galerkin scheme. Probabilistic Engineering Mechanics, 2014, 37:7-15, doi: 10.1016/j.probengmech.2014.03.006. [COBISS.SI-ID 6653793]

· KORELC, Jože, STUPKIEWICZ, Stanisław. Closed-form matrix exponential and its application in finite-strain plasticity. International journal for numerical methods in engineering, ISSN 0029-5981, 2014, 98(13):960-987, ilustr., doi: 10.1002/nme.4653. [COBISS.SI-ID 6526817]

· KORELC, Jože. Semi-analytical solution of path-independed nonlinear finite element models. Finite elem. anal. des., 2011, 47:281-287

· LENGIEWICZ, Jakub, KORELC, Jože, STUPKIEWICZ, Stanislaw., Automation of finite element formulations for large deformation contact problems. Int. j. numer. methods eng., 2011, 85: 1252–1279

· LAMUT, Martin, KORELC, Jože, RODIČ, Tomaž. Multiscale modelling of heterogeneous materials. Mater. tehnol., 2011, 45(5):421-426

· RODIČ, Tomaž, ŠUŠTAR, Tomaž, ŠUŠTARIČ, Primož, KORELC, Jože. Efficient numerical implementation of pressure, time and temperature superposition for elasto-visco-plastic material model by using a symbolic approach. Int. j. numer. methods eng., 2010, 84:470-484

· KORELC, Jože, ŠOLINC, Urša, WRIGGERS, Peter. An improved EAS brick element for finite deformation. Comput. mech., 2010, 46:641-659

· STUPKIEWICZ, Stanislaw, LENGIEWICZ, Jakub, KORELC, Jože. Sensitivity analysis for frictional contact problems in the augmented Lagrangian formulation. Comput. methods appl. mech. eng.,  2010, 199:2165-2176.

· KORELC, Jože. Direct computation of critical points based on Crout's elimination and diagonal subset test function. Comput. struct.. 2010, 88:189-197.

· KORELC, Jože. Automation of primal and sensitivity analysis of transient coupled problems. Comput. mech., 2009,  44:631-649.

· KRISTANIČ, Niko, KORELC, Jože. Optimization method for the determination of the most unfavorable imperfection of structures. Comput. mech., 2008, 42:859-872.

· KORELC, Jože. Automation of the finite element method. V: WRIGGERS, Peter. Nonlinear finite element methods. Berlin: Springer, 2008, 483-508.

· RODIČ, Tomaž, KORELC, Jože, PRISTOVŠEK, Anton. A micro-macro analysis of the tool damage in precision forming. Mater. tehnol., 2006, 40:243-246.

· STADLER, Michael, HOLZAPFEL, Gerhard A., KORELC, Jože. Cn continuous modelling of smooth contact surfaces using NURBS and application to 2D problems. Int. j. numer. methods eng., 2003, 57:2177-2203.

· BRANK, Boštjan, KORELC, Jože, IBRAHIMBEGOVIĆ, Adnan. Dynamic and time-stepping schemes for elastic shells undergoing finite rotations. Comput. struct., 2003, 81:1193-1210.

· STUPKIEWICZ, Stanislaw, KORELC, Jože, DUTKO, Martin, RODIČ, Tomaž. Shape sensitivity analysis of large deformation frictional contact problems. Comput. methods appl. mech. Eng, 2002, 191:3555-3581.

· KUNC, Robert, PREBIL, Ivan, RODIČ, Tomaž, KORELC, Jože. Low cycle elastoplastic properties of normalised and tempered 42CrMo4 steel, Materials Science and Technology, 2002, 18:1363-1368.

· KRSTULOVIĆ-OPARA, Lovre, WRIGGERS, Peter, KORELC, Jože. A C1-continuous formulation for 3D finite deformation frictional contact. Comput. mech., 2002, 29:27-42.

· KORELC, Jože, Multi-language and Multi-environment Generation of Nonlinear Finite Element Codes,  Engineering with Computers, 2002, 18(4):312-327

· BRANK, Boštjan, KORELC, Jože, IBRAHIMBEGOVIĆ, Adnan. Nonlinear shell problem formulation accounting for through-the-tickness stretching and its finite element implementation. Comput. struct., 2002, 80:699-717.

· WRIGGERS, Peter, KRSTULOVIĆ-OPARA, Lovre, KORELC, Jože. Smooth C1-interpolations for two-dimensional frictional contact problems. Int. j. numer. methods eng., 2001, 51:1469-1495.

· KORELC, Jože, WRIGGERS, Peter. Improved enhanced strain four-node element with Taylor expansion of the shape functions. Int. j. numer. methods eng., 1997, 40:407-421.

· KORELC, Jože, WRIGGERS, Peter. Consistent gradient formulation for a stable enhanced strain method for large deformations. Eng. comput., 1996, 13:103-123.

· KORELC, Jože. Automatic generation of finite-element code by simultaneous optimization of expressions. Theor. comput. sci.. , 1997, 187:231-248.

· WRIGGERS, Peter, KORELC, Jože. On enhanced strain methods for small and finite deformations of solids. Comput. mech., 1996, 18:413-428.

· KORELC, Jože, WRIGGERS, P. An efficient 3D enhanced strain element with Taylor expansion of the shape functions. Comput. mech., 1994, 19:20-40.