AceGen input for Timoschenko beam element, kinematically exact continuum beam theory

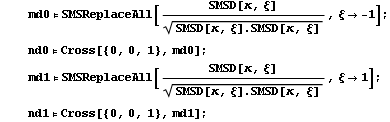
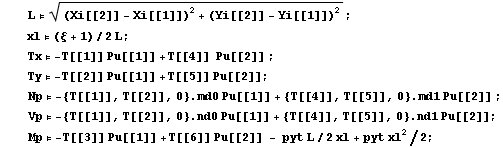
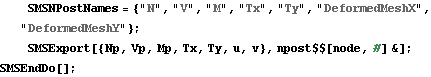
SMSWrite[];

AceFEM  Environment for 2D structural analysis

Requirements:
⇒    easy determination of boundary conditions
⇒    advaced posprocessing:-smooth displacements
⇒    standard display of loads and supports
⇒    standard tasks included

Boundary conditions, load

SMTConstrain[
  {list of nodes}
  ,index of dof to constrain
  , dof value :   0 unconstrained
                      - 1 permanent constrain
                      - 2 temporarily constrain (operator split)
]

BeamNodeData[i_]:=BeamNodeData[True&,i]

BeamNodeData[i_,j_]:=
SMTNodeData[
  If[Head[i]=!=Function
    ,Print["Beam environment: wrong parameter:",i];SMCAbort[];
    ,Replace[i,Function[k_]:→Function[k && "ID"=="DFi"]]
  ],
  Switch[j,"Fx","dB","Fy","dB","Mz","dB","Fx0","Bp","Fy0","Bp","Mz0","Bp",
   "u","at","v","at","φ","at","u0","Bp","v0","Bp","φ0","Bp"
   ,_,Print["Beam environment: Unknown keyword: ",j];SMCAbort[];],
  "Part"->Switch[j,"Fx",1,"Fy",2,"Mz",3,"Fx0",1,"Fy0",2,"Mz0",3,
  "u",1,"v",2,"φ",3,"u0",1,"v0",2,"φ0",3]
  ];

BeamNodeData[i_,j_,b_]:=Block[{selnode},
If[Head[i]=!=Function
    ,Print["Beam environment: wrong parameter:",i];SMCAbort[];
];
selnode=SMTFindNodes[Replace[i,Function[k_]:→Function[k && "ID"=="DFi"]]];
SMTNodeData[
  selnode
  ,Switch[j,"Fx","dB","Fy","dB","Mz","dB","Fx0","Bp","Fy0","Bp","Mz0","Bp"
   ,"u",SMTConstrain[selnode,1,-1];"dB"
   ,"v",SMTConstrain[selnode,2,-1];"dB"
   ,"φ",SMTConstrain[selnode,3,-1];"dB"
   ,"u0",SMTConstrain[selnode,1,-1];"Bp"
   ,"v0",SMTConstrain[selnode,2,-1];"Bp"
   ,"φ0",SMTConstrain[selnode,3,-1];"Bp"
   ,_,Print["Beam environment: Unknown keyword: ",j];SMCAbort[];
   ]
  ,b
  ,"Part"->Switch[j,"Fx",1,"Fy",2,"Mz",3,"Fx0",1,"Fy0",2,"Mz0",3,
           "u",1,"v",2,"φ",3,"u0",1,"v0",2,"φ0",3]
  ];
]

BeamFindElements[i_]:=SMTFindElements[i,Not[FreeQ[SMTDomainData[#,"CharSwitch"],"BeamEnvironment"]]&]

BeamElementData[i_,"LeftHinge"]:=
   Map[(
      SMTConstrain[SMTElements[[#,3,3]],1,0];
      AppendTo[SMTGraphicsElements,{#,BeamAdditionalGraphics}];
     )&,BeamFindElements[i]
   ];

BeamElementData[i_,"RightHinge"]:=
   Map[(
      SMTConstrain[SMTElements[[#,3,4]],1,0];
      AppendTo[SMTGraphicsElements,{#,BeamAdditionalGraphics}];
     )&,BeamFindElements[i]
   ];

BeamElementData[i_,j_,k_]:=Map[(
  AppendTo[SMTGraphicsElements,{#,BeamAdditionalGraphics}];
  Switch[j
   ,"px",SMTElementData[#,"Data",k,"Part"->1]
   ,"py",SMTElementData[#,"Data",k,"Part"->2]
   ,"mz",SMTElementData[#,"Data",k,"Part"->3]
   ,"px0",SMTElementData[#,"hp",k,"Part"->1]
   ,"py0",SMTElementData[#,"hp",k,"Part"->2]
   ,"mz0",SMTElementData[#,"hp",k,"Part"->3]
   ,_,SMCError=j;SMCAbort["Wrong keyword.","BeamSurfaceLoad",""];
  ]
  )&,BeamFindElements[i]];

BeamElementData[i_,j_]:=
SMTElementData[
   BeamFindElements[i]
  ,Switch[j
     ,"px","Data","py","Data","mz","Data","px0","hp","py0","hp","mz0","hp"
     ,_,SMCError=j;SMCAbort["Wrong keyword.","BeamElementData",""];
   ]
  ,"Part"->Switch[i,"px",1,"py",2,"mz",3,"px0",1,"py0",2,"mz0",3]
];

BeamElementData[i_]:=BeamElementData[True&,i]

Postprocessing

SMSAdditionalGraphics[
   {element index,domain index, list of nodes},
     True if node marks are required,
     True if boundary conditions are required,
     list of node coordinates for all element nodes
]
- returns empty list ({}) or list of graphics primitives

BeamAdditionalGraphics[e_,m_,b_,n_]:=
If[b
,{
   (* sufrace load *)
   If[Chop[Plus@@Abs[SMTElementData[e[[1]],"Data"]]]=!=0,
      { Switch[Map[Abs[#]>0&,SMTElementData[e[[1]],"Data"]],
        {True,False,False},RGBColor[1, 0.501961, 0],{False,True,False},RGBColor[0.501961, 1, 0],
        {False,False,True},RGBColor[1, 0, 0.501961],_,RGBColor[0.501961, 1, 0.501961]],
        AbsoluteThickness[2],
        Map[
         Line[
          {
          Offset[ 3 {-1,1} ((#[[2]]-#[[1]])/Sqrt[(#[[2]]-#[[1]]).(#[[2]]-#[[1]])])[[{2,1}]],#[[1]] ],
          Offset[ 3 {-1,1} ((#[[2]]-#[[1]])/Sqrt[(#[[2]]-#[[1]]).(#[[2]]-#[[1]])])[[{2,1}]],#[[2]] ]
         }]&,{n[[{1,3}]],n[[{3,4}]],n[[{4,5}]],n[[{5,6}]],
         n[[{6,7}]],n[[{7,8}]],n[[{8,9}]],n[[{9,10}]],n[[{10,11}]],n[[{11,2}]]}
        ]
        },{}],
    (* LeftHinge *)
    If[SMTNodeData[e[[3,3]],"DOF"][[1]]>=0,{RGBColor[1,0,0],
        AbsolutePointSize[6],Point[Offset[
            5 (n[[2]]-n[[1]])/Sqrt[(n[[2]]-n[[1]]).(n[[2]]-n[[1]])] ,n[[1]]]]},{}]
     (* RightHinge*)
    ,If[SMTNodeData[e[[3,4]] ,"DOF"][[1]]>=0,{RGBColor[1,0,0],
        AbsolutePointSize[6],
        Point[Offset[ -5 (n[[2]]-n[[1]])/
                Sqrt[(n[[2]]-n[[1]]).(n[[2]]-n[[1]])] ,n[[2]]]]},{}]
  }
,{}
]

SMTDrawEssentialBoundary[
   {x,y,z} ..node coordinates
   ,{dof1,dof2, }  True-essential False -natural
   ,NodeID
  ]
  - returns graphics primitive

SMTDrawEssentialBoundary[i_,j_,"DFi"]:=(
  Switch[j
      ,{True,True,True},
          {RGBColor[0,0,0],AbsoluteThickness[3],
           Line[{Offset[{-4,0},i],Offset[{4,0},i]}],Line[{Offset[{0,-4},i],Offset[{0,4},i]}]}
      ,{True,True,False},
          {RGBColor[0,0,0],AbsoluteThickness[2],
           Line[{i,Offset[{-5,-9},i],Offset[{5,-9},i],i}]}
      ,{True,False,False},
          {RGBColor[0,0,0],AbsoluteThickness[2],
           Line[{i,Offset[{7,-5},i],Offset[{7,5},i],i}],
            Line[{Offset[{11,-5},i],Offset[{11,5},i]}]}
      ,{False,True,False},
          {RGBColor[0,0,0],AbsoluteThickness[2],
           Line[{i,Offset[{-5,-7},i],Offset[{5,-7},i],i}],
            Line[{Offset[{-5,-11},i],Offset[{5,-11},i]}]}
      ,{True,False,True},
          {RGBColor[0,0,0],AbsoluteThickness[2],
           Line[{Offset[{-3,-7},i],Offset[{-3,7},i]}],
           Line[{Offset[{3,-7},i],Offset[{3,7},i]}]}
      ,{False,True,True},
          {RGBColor[0,0,0],AbsoluteThickness[2],
           Line[{Offset[{-7,-3},i],Offset[{7,-3},i]}],
           Line[{Offset[{-7,3},i],Offset[{7,3},i]}]}
      ,{False,False,True},
          {RGBColor[0,0,0],AbsoluteThickness[2],
           Line[{Offset[{-7,-3},i],Offset[{7,-3},i]}],
           Line[{Offset[{-7,3},i],Offset[{7,3},i]}],
           Line[{Offset[{-3,-7},i],Offset[{-3,7},i]}],
           Line[{Offset[{3,-7},i],Offset[{3,7},i]}]}
     ,_,{}
  ])

BeamShowMesh["All",j___Rule]:=Module[{q1,q2,q3},

q1={Max[#[[1]]]-Min[#[[1]]],Max[#[[2]]]-Min[#[[2]]]}&[Transpose[SMTNodeData["X"]]];

q3={"Legend"->False,"Show"->False,"TextStyle"->{FontSize->12,FontFamily->"Times"},j};

q2=Join[
{SMTShowMesh["DeformedMesh"->True,"Show"->False,
"Label"->StyleForm[
  "Max[|u|]="<>SMTNumberForm[Sqrt[SMTPost["DeformedMeshX"]^2+SMTPost["DeformedMeshY"]^2]//Max,6]<>
   "  Max[|φ|]="<>SMTNumberForm[Abs[BeamNodeData["φ"]]//Max,6]<>"\n",FontSize->12,FontWeight->"Plain"],
   "TextStyle"->{FontSize->12,FontFamily->"Times",FontWeight->"Bold"},
   "Marks"->True,"BoundaryConditions"->True,"NodeTagOffset"->{0.05, 0.05, 0.05},Sequence@@q3]},
If[Chop[SMTPost["N"]//Abs//Max]==0
  ,{}
  ,{SMTShowMesh["Field"->SMTPost["N","Smooth"->False],"Label"->{"N: ",Automatic},Sequence@@q3]}
],
If[Chop[SMTPost["V"]//Abs//Max]==0
  ,{}
  ,{SMTShowMesh["Field"->SMTPost["V","Smooth"->False],"Label"->{"V: ",Automatic},Sequence@@q3]}
],
If[Chop[SMTPost["M"]//Abs//Max]==0
  ,{}
  ,{SMTShowMesh["Field"->SMTPost["M","Smooth"->False],"Label"->{"M: ",Automatic},"LineFieldScale"->-1,Sequence@@q3]}
]
];


Grid[Join[{{StyleForm[StringJoin[
      "Results of static analysis for γ=",ToString[SMTRData["Multiplier"]]],FontSize->14],
  SpanFromLeft}}, Partition[q2, 2, 2, 1, ""]]]

]

BeamShowMesh["N",i___Rule]:=SMTShowMesh[i,"Field"->SMTPost["N","Smooth"->False],"Legend"->"MinMax",
"Label"->StyleForm["Axial force N",FontSize->14]];
BeamShowMesh["M",i___Rule]:=SMTShowMesh[i,"Field"->SMTPost["M","Smooth"->False],"Legend"->"MinMax",
"Label"->StyleForm["Bending moment M",FontSize->14],"LineFieldScale"->-1];
BeamShowMesh["V",i___Rule]:=SMTShowMesh[i,"Field"->SMTPost["V","Smooth"->False],"Legend"->"MinMax",
"Label"->StyleForm["Shear force V",FontSize->14]];
BeamShowMesh["Tx",i___Rule]:=SMTShowMesh[i,"Field"->SMTPost["Tx","Smooth"->False],"Legend"->"MinMax",
"Label"->StyleForm["Force Tx",FontSize->14]];
BeamShowMesh["Ty",i___Rule]:=SMTShowMesh[i,"Field"->SMTPost["Ty","Smooth"->False],"Legend"->"MinMax",
"Label"->StyleForm["Force Ty",FontSize->14]];
BeamShowMesh["u",i___Rule]:=SMTShowMesh[i,"DeformedMesh"→True,"BoundaryConditions"→True,
"Label"->{StyleForm["Displacements",FontSize→14]}];
BeamShowMesh[i___Rule]:=SMTShowMesh[i,"DeformedMesh"→True,"BoundaryConditions"→True,"Marks"->True];

Limit load analysis by bisection

BeamLimitLoadAnalysis[g0_, gMax_, e_]:=
Module[{stepnds},
SMTNextStep[1, g0];
While[
  While[step = SMTConvergence[10^(-9), 20, {"Adaptive", 8, g0/100, gMax/2, gMax}], SMTNewtonIteration[];];
  SMTStatusReport[nds=SMTIData["DiagonalSign"]];
  step[[3]] && nds == 0
,If[step[[1]], SMTStepBack[];];
  SMTNextStep[1, step[[2]]]
];
SMTStepBack[];
SMTNextStep[1, SMTRData["MultiplierIncrement"]/2];  
While[
While[step = SMTConvergence[10^(-8), 20, "Analyze"], SMTNewtonIteration[];];
SMTStatusReport[nds=SMTIData["DiagonalSign"]];
Abs[SMTRData["MultiplierIncrement"]] > Abs[e*SMTRData["Multiplier"]],
If[step =!= False || nds > 0, SMTStepBack[];];
SMTNextStep[1, SMTRData["MultiplierIncrement"]/2];
];
SMTStatusReport[SMTIData["DiagonalSign"]];
Print["Critical load factor (bisection) =", SMTRData["Multiplier"]];
SMTRData["Multiplier"]
]

Buckling analysis

Options[BeamBucklingAnalysis]={"Modes"->6,"ShowModes"->True};
BeamBucklingAnalysis[allopt___Rule]:=
Module[{K0, KG,eigs, nnotzero, bload, bshape, alldofs,q1,q2,at,opt},

   opt={"Modes","ShowModes","ShowDiagrams"}/.{allopt}/.Options[BeamBucklingAnalysis];

   If[And@@Map[Not[FreeQ[#,"GeometricTangentMatrix"]]&,SMTDomainData["CharSwitch"]]
    ,SMTNewtonIteration[];
     SMTIData["GeometricTangentMatrix",1];
     K0=SMTData["TangentMatrix"];
     SMTIData["GeometricTangentMatrix",2];
     KG=SMTData["TangentMatrix"];
     SMTIData["GeometricTangentMatrix",0];
     SMTNewtonIteration[];
     SMTConvergence["Reset"];
     While[SMTConvergence[10^-8,10],SMTNewtonIteration[];];
    ,K0=SMTData["TangentMatrix"];
     While[SMTConvergence[10^-8,10],SMTNewtonIteration[];];
     KG=SMTData["TangentMatrix"]-K0;
   ];
   Off[Eigensystem::argpd];
   eigs=Re[Eigensystem[{K0,-KG},-opt[[1]]]];
   Onn[Eigensystem::argpd];
   bload=eigs[[1]]//Reverse;
   nnotzero=Min[opt[[1]], Length[bload]];
   bshape=eigs[[2]]//Reverse;
   alldofs=SMTNodeData["at"];
       
  q1={Max[#[[1]]]-Min[#[[1]]],Max[#[[2]]]-Min[#[[2]]]}&[Transpose[SMTNodeData["X"]]];
  q2=Table[
      at=MapIndexed[
           If[#1 < 0,Extract[alldofs, #2],bshape[[i,#1+1]]]&
         ,SMTNodeData["DOF"],{2}];
       SMTNodeData["at",at];
       SMTShowMesh["BoundaryConditions"->False,"DeformedMesh"->True,
         "Scale"->SMTRData["XYZRange"]/15/Max[Abs[{SMTPost["DeformedMeshX"],SMTPost["DeformedMeshY"]}],1/10^12],
         "Label"->{"Mode=",i," ",SubscriptBox["γ","CR"]//DisplayForm,"=",
          bload[[i]]},"Marks"-> False,"Show"->False
       ]
  ,{i,1,nnotzero}];
  SMTNodeData["at",alldofs];    
  Print[
    Grid[
      Join[
       {{Style[Row[{
         "Buckling analysis - first ", nnotzero, " buckling modes"}],
         FontSize -> 14], SpanFromLeft}},
       Partition[q2,3,3,1, ""]
      ]
    , Frame → All]
  ];
  bload
]

Created by Wolfram Mathematica 6.0  (12 August 2007)