A) Trial Lagrange polynomial interpolation

Definitions

A trial function for temperature φ is constructed as a fifth order Lagrange polynomial in x y and z direction. The chosen trial function is constructed in a way that  satisfies boundary conditions.

Here the fifth order Lagrange polynomials are constructed in three dimensions.

Here the Gauss points and weights are calculated for ngp×ngp×ngp Gauss numerical integration of the free energy over the domain [-.0.5m,0.5m]×[-0.5m,0.5m]×[0,1m].

Direct use of Mathematica

The subsection Definitions has to be executed before the current subsection.

G. Gradient based optimization

N. Newton method based optimization

AceGen code generation

The subsection Definitions has to be executed before the current subsection.

AceGen Solution

G. Gradient based optimization

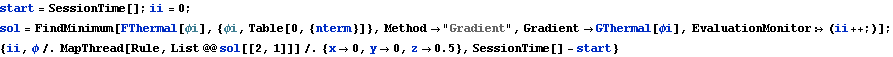
N. Newton method based optimization

Created by Wolfram Mathematica 6.0  (13 August 2007)