B) Finite difference interpolation

Definitions

The central difference approximation of derivatives is used for the points inside the cube and backward or forward difference for the points on the boundary.

Direct use of Mathematica

The subsection Definitions have to be executed before the current subsection.

G. Gradient based optimization

N. Newton method based optimization

AceGen code generation

The subsection Definitions have to be executed before the current subsection.

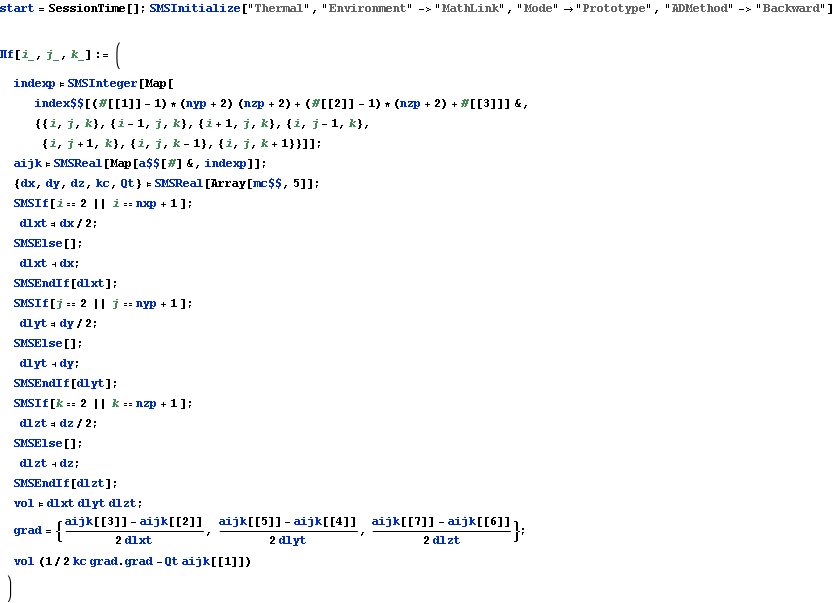
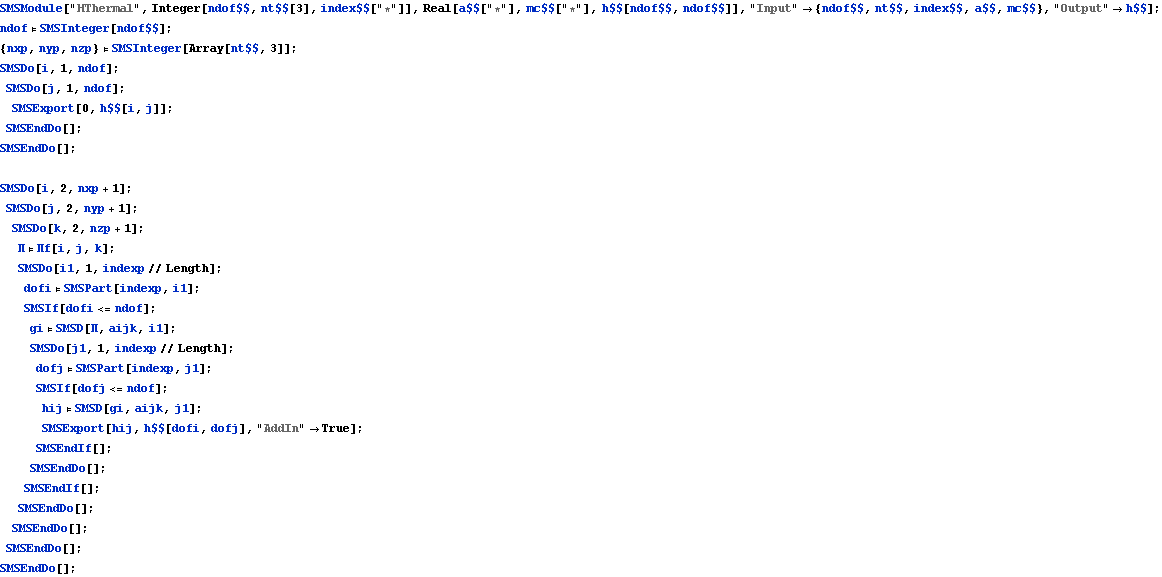
AceGen Solution

G. Gradient based optimization

N. Newton method based optimization

The tangent matrix is in the case of finite difference approximation extremely sparse.

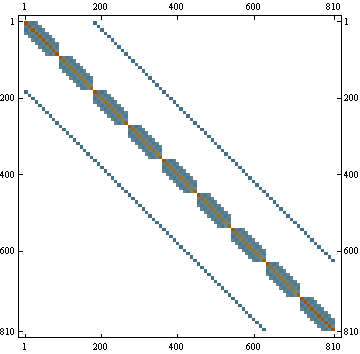
Created by Wolfram Mathematica 6.0  (13 August 2007)