Description of snooker simulation

Analyze a single snooker shoot as depicted under the following assumptions:

2D problem

plane strain condition and hyperelastic material

4 node element

Newmark's time integration

2D smooth deformable-deformable contact with Coulomb friction

augmented Lagrange multipliers method

Example has been contributed by Jakub Lengiewicz, Institute of Fundamental Technological Research, Warszawa, Poland.

Out[525]=

Hypersolid dynamic element

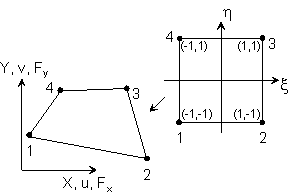
Generate two-dimensional, four node finite element for the analysis of the steady state problems in the mechanics of solids. The element has the following characteristics:
⇒    quadrilateral topology,
⇒    4 node element,
⇒    isoparametric mapping from the reference to the actual frame,

⇒    global unknowns are displacements of the nodes,
⇒    the element should allow arbitrary large displacements and rotations,
⇒    the problem is defined by the hyperelastic Neo-Hooke type strain energy potential,
    ,
    where is right Cauchy-Green tensor, F=I+▽u  is deformation gradient,
    u is displacements field, Q is prescribed body force, t is prescribed surface traction,
     is the initial domain of the problem and λ, μ are the first and the second Lame's material constants.
    
⇒    The Newmark's time integration
    = + (1-) dt ,
    = - (-1) dt ,
    β , γ ...Newmark's - constants
    
The following user subroutines have to be generated:
⇒    user subroutine for the direct implicit analysis,
⇒    user subroutine for the  post-processing that returns the Green-Lagrange strain tensor and
    the Cauchy stress tensor.

Smooth master segment contact element

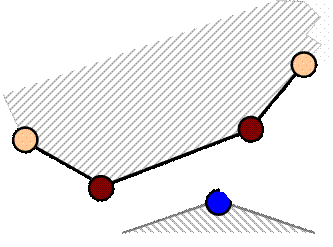
Node-to-segment smooth element for analysis of the 2-D contact problems has the following characteristics:
⇒    8 node element: one slave node + two dummy slave nodes (referential area) + four master nodes (3rd order Bezier curve) + lagrange multipliers node,
⇒    global unknowns are displacements of the nodes + lagrange multipliers,
⇒    the element should allow arbitrary large displacements,
⇒    the impenetrability condition is regularized with augmented lagrange multipliers method and formulated as energy potential (for each node on slave contact surface):
        
    where:
        
    and
        
    and
        

     and ρ is regularisation parameter, is normal gap (at the point of orthogonal projection of slave point on master boundary), is tangential slip.
      and are lagrange multipliers and have a meaning of normal and tangential nominal pressure respectively.

The following user subroutines have to be generated:
⇒    user subroutine for specification of  nodal positions,
⇒    user subroutine for the direct implicit analysis,

Created by Wolfram Mathematica 6.0  (13 August 2007)